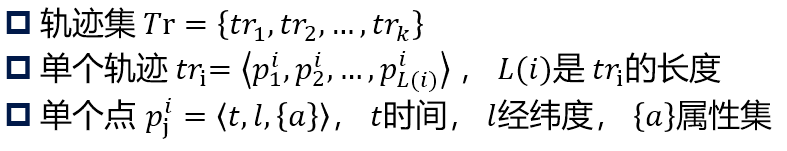论文:Clustering Trajectories by Relevant Parts for Air Traffic Analysis
作者:Gennady Andrienko, Natalia Andrienko, Georg Fuchs, and Jose Manuel Cordero Garci
发表:IEEE VAST 2017
简介
针对不同的分析任务,研究人员会对轨迹中的不同部分感兴趣,例如在研究起飞、降落计划时,只有轨迹中的起始与结束阶段是有用的。对数据中与与分析任务有关的部分进行聚类,叫做相关聚类(Relevance-aware Clustering)。一般情况下,相关聚类只需要提前把数据处理好,过滤掉数据中的无关部分,存储处理好的数据即可,但是在分析过程中对相关与不相关的判断会不断发生变化。因此,本文针对轨迹的相关聚类,提出了一套完整的工作流程与分析方法。文章所用的数据集为飞行轨迹数据,但文章提出的方法适用于其他所有类型的轨迹。
工作流程
- 符号定义:
- 流程:
- 过滤:
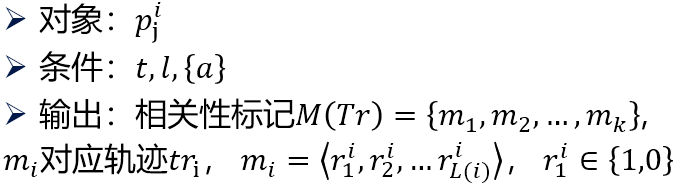
- 聚类:使用基于密度的聚类算法,选择合适的轨迹距离函数 D(tr_1,m_1,tr_2,m_2)对过滤后的轨迹进行聚类。
- 总结与分析:为每个聚类构造一个具有总结性的表征代表这个聚类,并对聚类结果进行可视分析。
过滤
提出特殊的交互式过滤方法并不是本文的目标,任何已有方法及其组合都是可用的,只需要满足:
- 能够单独观察轨迹中的相关部分
- 能够单独观察轨迹中的不相关部分
- 能够在不相关部分的基础上观察相关部分
为此,本文提出了三种可视化方案以满足上述需求:
- Filter-aware rendering:用不同的线属性区分轨迹中的相关与不相关部分,例如,实线、虚线,或粗线、细线,不透明、带透明度的线等。
- Visualization of Boolean attribute:赋予过滤后的每个点一个布尔值,true 或者 false,分别表示相关与不相关,可视化时用不同颜色的线进行区分。
- Different level of detail:轨迹中相关的部分展示全部细节,不相关的部分则只展示聚合结果,下图用了 hill shading 的技术将不相关部分展示为密度表面。

聚类
本文采用基于密度的聚类算法 Optics,算法的大致过程如下:
- 符号定义

- 算法过程:遍历轨迹集中的所有点,确定哪些点是核心点,并将其他到核心点距离小于核心距离的点定义为直接可达点,存储每个核心点的直接可达点并按照距离排序。遍历每个核心点的直接可达点集合,判断该点是否为核心点,若是,则将其直接可达点集合加入原有集合。
- 距离函数:route similarity
- 聚类方式:渐进式聚类,通过不断调整范围半径与最少点数两个参数优化聚类结果。
总结与分析
本文使用一个聚类的中心轨迹(central trajectory of each cluster, CTC)来表征一个聚类的特征,本文提出的方法考虑地理位置上的相似性,并考虑到了相关性标记(计算时只考虑标记为有效的点)。算法分为对分与调整两个部分:
- 对分:首先将一类轨迹的起点归为组 1,重点归为组 2,接着将每条轨迹中位于起点与终点中间位置的点,归为组 3,接着寻找组 1 与组 3,组 2 与组 3 的中间组,依次类推对轨迹进行二分。
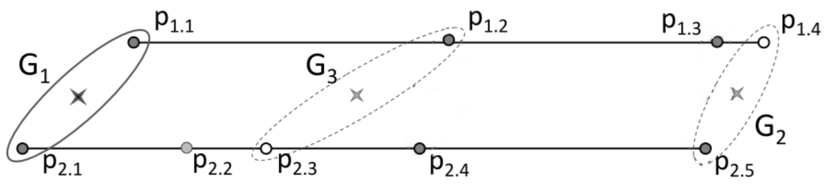
- 调整:完成分组后,计算每组中心(所有点坐标的平均数或中位数),找到轨迹中未被分组的点,判断该点到附近组中心的距离是否比该轨迹上在该组内的点离中心更新,若是,则用该点替代原有分组内的点并重新计算计算组的中心。
计算完成后,按照组的前后顺序,连接各组中心作为该类的中心轨迹。
评估
本文邀请了两位领域专家,进行了三个案例的分析作为本文提出的轨迹聚类的定性评估。这里将介绍其中的一个案例,如何进行飞行路线选择。
对于拥有相同出发地与目的地的航班而言,如何选择飞行路线是一件困难的事情,因为在穿过不同国家时收取的导航费与税费标准是不同的,且收取标准按照进入国界到出国界穿越的距离计算。本案例的研究目的为探究这些收费标准是如何影响飞行员进行路线选择的。案例用到的数据为 2016 年 1 月-5 月,巴黎至伊斯坦布尔的 6 位操作员制定的不同飞行路线,收费标准按 x 欧元/(100 公里,50 吨重量)计算,数据集中共 1,717 条计划飞行路线,122,793 个位置点,实际飞行路线与计划路线有个别偏离情况,共 171,134 个位置点。
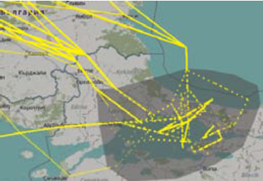
首先,为了找到 1,717 条路线中的主要飞行路线,需要过滤掉轨迹中的起飞与降落阶段,因为可用跑道不同或天气状况造成的不同操作流程,会导致对具有总体一致路线的航班,起飞与降落路径是不同的。可以通过在地图上刷选起飞与降落区域的机场范围来达到过滤目的,如下图: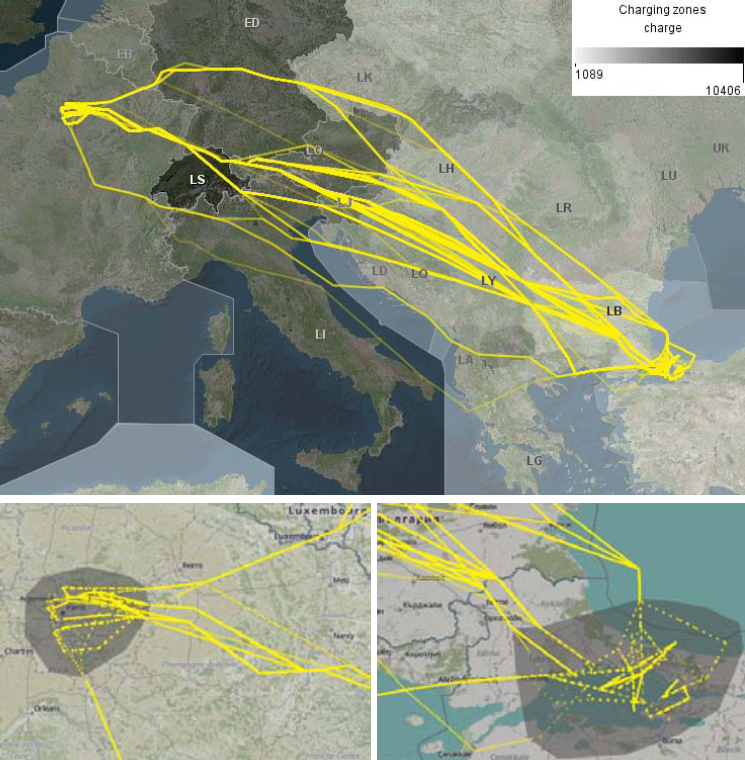
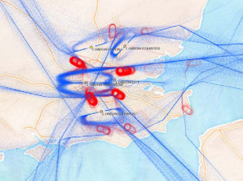
过滤完成后,需要对过滤后的轨迹进行聚类,作者尝试了不同的聚类参数,发现有一个超大类(包含轨迹数量特别多)。为了达到更好的聚类效果,作者采用渐进式聚类,先通过一次聚类找到数量最大的类 (ϵ=3km, MinPts=10),再调整参数,对除最大类以外的所有轨迹进行聚类(ϵ=6km, MinPts=10),最后共得到 9 类,包含 1,626 条轨迹 (94.7%,其余轨迹为噪音),其中有 1,031 条属于最大类。下图为 9 类聚类的中心轨迹,颜色表示类别,轨迹的粗细表示类的大小: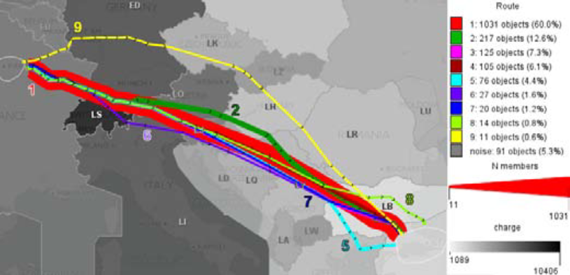
其次,领域专家对收费标准对路线选择的影响进行探究。下图中轨迹的粗细跟地图的灰色背景色的深浅均表示过路费标准的高低,轨迹越宽,灰度越深表示过路费越高。可以发现,瑞士的过路费相对较贵(LS),因此其他飞行线路都尽可能避免在瑞士开很远的距离,只有六号线路(紫色)在瑞士开的路线比较长。此外,离开瑞士以后,路线 2(绿色)偏离了其他路线,往奥地利(LO)跟匈牙利(LH)方向行驶,因此避开了过路费更贵的意大利(LI)、斯洛文尼亚(LJ)、克罗地亚(LD)等区域,为所有线路中飞行成本最低的线路。
讨论
本文的主要贡献为提出的轨迹相关聚类方法流程,对应案例分析作为唯一的定性评估。但是用中心轨迹作为一个聚类的表征只局限于地理形状相近的轨迹,无法考虑时间维度上的相似性。
✉️ zhangtianye1026@zju.edu.cn